La Ragione Fisica dell’Incertezza Quantistica, Un Viaggio nel Meraviglioso Mondo dei Quanti
Come vorrei che le persone si interessassero di tutto quanto riguarda la scienza……..ma quella ricca di costanti incertezze e non quella che ci è dato a credere sia la verità assoluta! (Toba60)
Questo lavoro comporta tempo e denaro e senza fondi non possiamo dare seguito ad un progetto che dura ormai da anni, sotto c’è un logo dove potete contribuire a dare seguito a qualcosa che pochi portali in Italia e nel mondo offrono per qualità e affidabilità di contenuti unici nel loro genere.
La Ragione Fisica dell’Incertezza Quantistica
A prescindere dalla qualità dei nostri dispositivi di misurazione, alcune proprietà quantistiche possiedono sempre un’incertezza intrinseca. Possiamo capire perché?
Oggi l’Universo si è evoluto nel luogo complesso e favorevole alla vita che conosciamo perché siamo stati in grado di formare atomi neutri fin dalle prime fasi dell’Universo. Tuttavia, senza le giuste proprietà quantistiche, la formazione di atomi stabili e neutri sarebbe stata ritardata in modo significativo o addirittura non sarebbe avvenuta affatto.

Punti di forza
1) Indipendentemente dal modo in cui si tenta di misurare o calcolare certe proprietà quantistiche, sarà sempre presente un’incertezza intrinseca che renderà impossibile una conoscenza completa di tale sistema.
2) Ma da dove deriva questa incertezza? È una proprietà inerente alle particelle o c’è qualche altra causa sottostante che non siamo ancora riusciti a scoprire?
3) Potrebbe avere a che fare con i campi quantistici inerenti allo spazio vuoto stesso? O questo non fa che spostare il problema noto in un territorio sconosciuto?
Forse la proprietà più bizzarra che abbiamo scoperto sull’Universo è che la nostra realtà fisica non sembra essere governata da leggi puramente deterministiche. Al contrario, a un livello fondamentale, quantistico, le leggi della fisica sono solo probabilistiche: si può calcolare la probabilità dei possibili risultati sperimentali che si verificheranno, ma solo misurando la quantità in questione si può veramente determinare cosa sta facendo il sistema in quell’istante. Inoltre, l’atto stesso di misurare/osservare determinate quantità comporta un aumento dell’incertezza in alcune proprietà correlate: quelle che i fisici chiamano variabili coniugate.
Sebbene molti abbiano avanzato l’idea che l’incertezza e l’indeterminismo siano solo apparenti e possano essere dovuti a variabili “nascoste” che sono davvero deterministiche, non abbiamo ancora trovato un meccanismo che ci permetta di prevedere con successo qualsiasi risultato quantistico. Ma i campi quantistici inerenti allo spazio potrebbero essere il colpevole finale? Questa è la domanda di questa settimana di Paul Marinaccio, che vuole saperlo:
“Mi sono chiesto per molto tempo: il vuoto quantistico fornisce il qualunque per le vibrazioni dei pacchetti di onde delle particelle. Si comporta… come si pensava facesse l’etere? So che questo è un modo molto semplificato di porre la domanda, ma non so come esprimerla in termini matematici”.
Diamo un’occhiata a ciò che l’Universo ha da dire su questa idea. Eccoci qua!
In fisica quantistica, ci sono due modi principali di pensare all’incertezza. Uno è: “Ho creato il mio sistema con queste particolari proprietà, e quando tornerò in un momento successivo, cosa potrò dire di quelle proprietà?”. Per alcune proprietà – come la massa di una particella stabile, la carica elettrica di una particella, il livello di energia di un elettrone legato allo stato fondamentale del suo atomo, eccetera – queste proprietà rimarranno invariate. Finché non ci saranno altre interazioni tra la particella quantistica e l’ambiente circostante, queste proprietà rientreranno chiaramente nel campo del noto, senza alcuna incertezza.
Ma altre proprietà sono meno certe. Se si colloca un elettrone libero nello spazio in una posizione nota con precisione, quando si torna indietro, la posizione dell’elettrone non può più essere conosciuta in modo definitivo: la funzione d’onda che descrive la sua posizione si espande nel tempo. Se si vuole sapere se una particella instabile è decaduta, lo si può scoprire solo misurando le proprietà di quella particella e vedendo se è decaduta o meno. E se si chiede quale fosse la massa di una particella instabile decaduta radioattivamente, che si può ricostruire misurando l’energia e la quantità di moto di ciascuna delle particelle in cui è decaduta, si otterrà una risposta leggermente diversa da evento a evento, incerta e dipendente dalla durata di vita della particella.

L’ampiezza intrinseca, ovvero la metà dell’ampiezza del picco nell’immagine qui sopra quando si è a metà della cresta del picco, è misurata in 2,5 GeV: un’incertezza intrinseca di circa il +/- 3% della massa totale. La massa della particella in questione, il bosone Z, ha un picco di 91,187 GeV, ma questa massa è intrinsecamente incerta di una quantità significativa a causa della sua vita troppo breve. Questo risultato è straordinariamente coerente con le previsioni del Modello Standard.
Si tratta di una forma di incertezza che sorge a causa dell’evoluzione temporale: perché la natura quantistica della realtà fa sì che certe proprietà possano essere conosciute solo con una certa precisione. Con il passare del tempo, questa incertezza si propaga nel futuro, portando a uno stato fisico che non può essere arbitrariamente noto.
Ma c’è un altro modo in cui nasce l’incertezza: perché certe coppie di grandezze, quelle variabili coniugate, sono correlate in modi in cui conoscerne una con maggiore precisione intrinsecamente
riduce la conoscenza che si può avere dell’altra. Questo deriva direttamente dal principio di indeterminazione di Heisenberg, e si manifesta in un’ampia varietà di situazioni.
L’esempio più comune è quello del rapporto tra posizione e quantità di moto. Quanto meglio si misura la posizione di una particella, tanto meno si è in grado di sapere quale sia la sua quantità di moto: quanto veloce e in quale direzione sia la sua “quantità di moto”. Questo ha senso se si pensa a come si effettua una misurazione della posizione: provocando un’interazione quantistica tra la particella che si sta misurando e un altro quanto, con o senza massa a riposo. In entrambi i casi, alla particella può essere assegnata una lunghezza d’onda; le particelle più energetiche hanno lunghezze d’onda più corte e quindi possono misurare una posizione con maggiore precisione.

Le scale di dimensione, lunghezza d’onda e temperatura/energia che corrispondono alle varie parti dello spettro elettromagnetico. Per sondare le scale più piccole è necessario andare a energie più elevate e a lunghezze d’onda più corte. La luce ultravioletta è sufficiente a ionizzare gli atomi, ma con l’espansione dell’Universo la luce si sposta sistematicamente verso temperature più basse e lunghezze d’onda maggiori.
Ma se si stimola una particella quantistica facendola interagire con un’altra particella quantistica, ci sarà uno scambio di quantità di moto tra le due. Maggiore è l’energia della particella che interagisce:
- quanto più breve è la sua lunghezza d’onda,
- che porta a una posizione più conosciuta,
- ma anche a una maggiore quantità di energia e di momento impartiti alla particella,
- che porta a una maggiore incertezza nella sua quantità di moto.
Potreste pensare di poter fare qualcosa di intelligente per “imbrogliare” questo problema, come ad esempio misurare la quantità di moto della particella in uscita che avete usato per determinare la posizione della particella, ma ahimè, questo tentativo non vi salverà.
C’è una quantità minima di incertezza che si conserva sempre: il prodotto dell’incertezza in ciascuna delle due quantità deve sempre essere maggiore o uguale a un valore specifico. Per quanto si possa misurare bene la posizione (Δx) e/o la quantità di moto (Δp) di ogni particella coinvolta in queste interazioni, il prodotto della loro incertezza (ΔxΔp) è sempre maggiore o uguale alla metà del costante di Planck ridotta, ħ/2.

Questo diagramma illustra la relazione di incertezza intrinseca tra posizione e quantità di moto. Quando una delle due è conosciuta con maggiore precisione, l’altra è intrinsecamente meno in grado di essere conosciuta con precisione. Ogni volta che si misura con precisione una delle due grandezze, si assicura una maggiore incertezza nella corrispondente grandezza complementare.
Ci sono molte altre quantità che presentano questa relazione di incertezza, non solo la posizione e la quantità di moto. Tra queste vi sono:
- orientamento e momento angolare,
- energia e tempo,
- lo spin di una particella in direzioni reciprocamente perpendicolari,
- potenziale elettrico e carica elettrica libera,
- potenziale magnetico e corrente elettrica libera,
È vero che viviamo in un universo quantistico, quindi ha senso, intuitivamente, chiedersi se non ci sia una sorta di variabile nascosta alla base di tutta questa “stranezza” quantistica. Dopotutto, molti hanno filosofeggiato sul fatto che la nozione di incertezza quantistica sia intrinseca, cioè una proprietà inestricabile della natura stessa, o se ci sia una causa sottostante che semplicemente non siamo stati in grado di individuare. Quest’ultimo approccio, favorito da molte grandi menti nel corso della storia (tra cui Einstein), è comunemente noto come ipotesi delle variabili nascoste.

La natura quantistica dell’Universo ci dice che alcune grandezze hanno un’incertezza intrinseca e che coppie di grandezze hanno le loro incertezze in relazione tra loro. Non ci sono prove di una realtà più fondamentale con variabili nascoste che sia alla base del nostro Universo osservabile e quantistico. Questa illustrazione mostra l’Universo primordiale come costituito da schiuma quantistica, dove le fluttuazioni quantistiche sono grandi, varie e importanti anche su scale minime.
Il modo in cui mi piace immaginare le variabili nascoste è come se l’Universo, e tutte le particelle che lo compongono, fossero seduti in cima a un piatto che vibra rapidamente e caoticamente, impostato sull’ampiezza più bassa. Quando si osserva l’Universo su grandi scale macroscopiche, non si vedono affatto gli effetti di questa vibrazione; sembra che lo “sfondo” dell’Universo in cui esistono tutte le particelle sia stabile, costante e privo di fluttuazioni.
Ma quando si scende a scale sempre più piccole, si nota la presenza di queste proprietà quantistiche. Le quantità fluttuano; le cose non rimangono perfettamente stabili e immutabili nel tempo; e quanto più si cerca di individuare una particolare proprietà quantistica, tanto più si troverà un’incertezza nella quantità coniugata ad essa associata.
È facile immaginare, sulla base del fatto che ci sono campi quantistici che permeano tutto lo spazio, anche quello completamente vuoto, che questi campi sottostanti siano essi stessi la fonte di tutto ciò. L’incertezza che vediamo, forse, nasce come conseguenza del vuoto quantistico.

Visualizzazione di un calcolo della teoria quantistica dei campi che mostra le particelle virtuali nel vuoto quantistico. Anche nello spazio vuoto, l’energia del vuoto non è nulla, ma senza specifiche condizioni al contorno, le proprietà delle singole particelle non saranno vincolate. Nello spazio curvo, il vuoto quantistico differisce dallo spazio piatto, proprio come un osservatore in accelerazione sperimenta un vuoto quantistico diverso da quello di un osservatore inerziale.
Non è certo un’idea facile da escludere, dato che il fatto dell’incertezza quantistica è “incorporato” nella nostra comprensione fondamentale delle particelle e dei campi. Ogni formulazione (che funzioni) della meccanica quantistica e della teoria quantistica dei campi la include, e la include a un livello fondamentale, non solo come un’aggiunta ad hoc a posteriori. In realtà, non sappiamo nemmeno come usare la teoria quantistica dei campi per calcolare quale sia il contributo complessivo al vuoto quantistico per ciascuna delle forze fondamentali; sappiamo solo, grazie alla misurazione dell’energia oscura, quale debba essere il contributo totale. Quando tentiamo di fare un calcolo di questo tipo, le risposte che otteniamo sono insensate e non ci forniscono alcuna informazione significativa.
Ma ci sono alcune informazioni che sarebbero difficili da spiegare con l’idea che le fluttuazioni nello spazio sottostante siano responsabili dell’incertezza quantistica e della diffusione dei pacchetti d’onda che osserviamo. Per esempio, si consideri ciò che accade quando si prende una particella quantistica che ha un momento angolare intrinseco (spin), la si lascia muovere nello spazio e le si applica un campo magnetico.
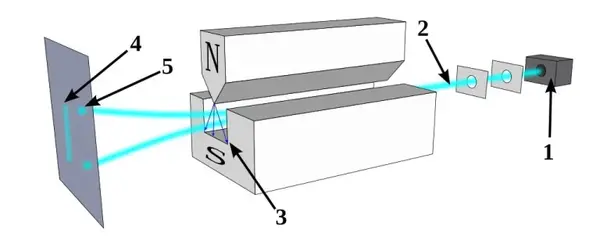
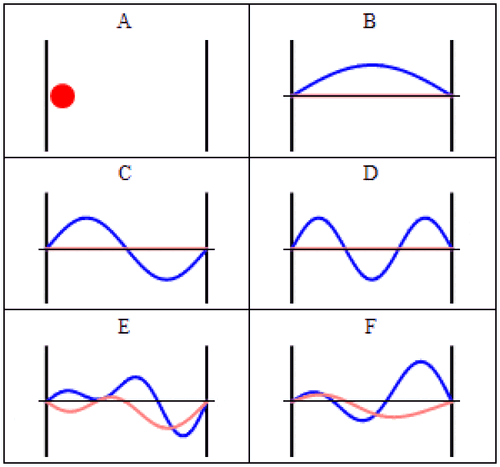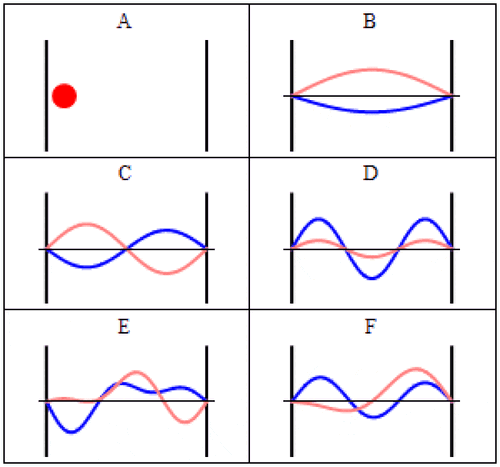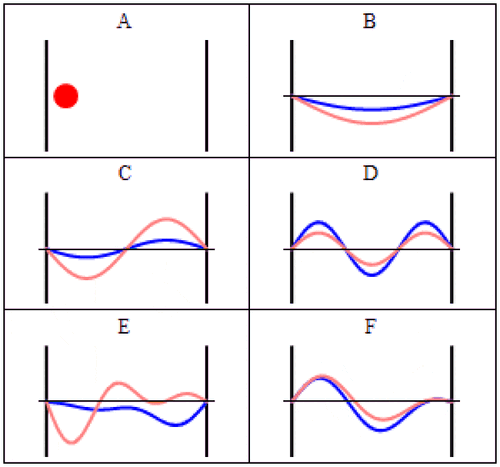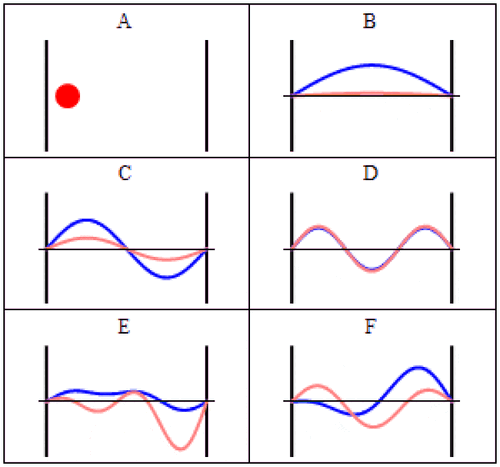
Nell’esperimento di Stern-Gerlach, qui illustrato, una particella quantistica con uno spin finito viene fatta passare attraverso un campo magnetico, che fa sì che lo spin diventi ben determinato in quella direzione: positivo (spin up) o negativo (spin down). Ogni particella prende una strada o l’altra e da quel momento non ha più incertezze nel suo spin lungo l’asse del campo magnetico applicato; si ottiene un insieme di valori discreti (5), non un continuum di valori (4) come ci si aspetterebbe se gli spin fossero orientati casualmente nello spazio tridimensionale.
La deflessione della particella sarà positiva o negativa: dipende dalla direzione del campo magnetico applicato e dal fatto che lo spin della particella sia orientato in direzione positiva o negativa. La deflessione avviene lungo la stessa dimensione in cui viene applicato il campo magnetico.
Ora applicate un campo magnetico in una direzione diversa, perpendicolare. Avete già determinato quale fosse lo spin in una particolare direzione, quindi cosa pensate che accadrà se applicate quel campo magnetico in una direzione diversa?
La risposta è che la particella devierà di nuovo, con una probabilità del 50/50 di essere allineata con la direzione del campo o di essere anti-allineata con la direzione del campo.
Ma non è questa la parte interessante. La parte interessante è che l’atto di effettuare quella misurazione, di applicare quel campo supplementare e perpendicolare, ha di fatto distrutto l’informazione ottenuta in precedenza applicando il primo campo magnetico. Se poi si applica lo stesso identico campo applicato durante la prima parte dell’esperimento, quelle particelle, anche se in precedenza erano tutte orientate positivamente, avranno di nuovo degli spin casuali: 50/50 allineati e anti-allineati con il campo.

Quando si fa passare un insieme di particelle attraverso un singolo magnete di Stern-Gerlach, queste devieranno secondo il loro spin. Se le si fa passare attraverso un secondo magnete perpendicolare, si dividono di nuovo nella nuova direzione. Se poi si torna alla prima direzione con un terzo magnete, si dividono ancora una volta, dimostrando che l’informazione determinata in precedenza è stata randomizzata dalla misura più recente.
È molto difficile dare un senso a tutto ciò partendo dal presupposto che il vuoto quantistico stesso sia responsabile dell’intera incertezza quantistica. In questo caso, il comportamento della particella dipende dal campo esterno che le è stato applicato e dalle successive interazioni che ha sperimentato, non dalle proprietà dello spazio vuoto che ha attraversato. Se si rimuove il secondo magnete dalla configurazione sopra descritta – quello orientato perpendicolarmente al primo e al terzo magnete – non ci sarebbe alcuna incertezza riguardo allo spin della particella nel momento in cui arriva al terzo magnete.
È difficile capire come lo stesso “spazio vuoto”, o il “vuoto quantistico” se preferite, possa essere responsabile dell’incertezza quantistica sulla base dei risultati di questo esperimento. Sono le interazioni (o la loro mancanza) che un sistema quantistico sperimenta a determinare il modo in cui l’incertezza quantistica si manifesta, non una proprietà inerente ai campi che permeano tutto lo spazio.
Che vi piaccia o no, la realtà di ciò che osservate dipende da come e se lo osservate; semplicemente ottenete risultati sperimentali diversi a causa delle specificità del vostro apparato di misura.

Gli elettroni presentano proprietà ondulatorie e particellari e possono essere utilizzati per costruire immagini o sondare le dimensioni delle particelle proprio come la luce. Qui si possono vedere i risultati di un esperimento in cui gli elettroni vengono sparati uno alla volta attraverso una doppia fenditura. Una volta sparati un numero sufficiente di elettroni, si può vedere chiaramente il modello di interferenza.
Ad oggi, non esiste alcuna teoria delle variabili nascoste che abbia prodotto prove sperimentali o osservative dell’esistenza di una realtà sottostante, oggettiva e indipendente dalle nostre misurazioni. Molti sospettano che ciò sia vero, ma ciò si basa sull’intuizione e sul ragionamento filosofico: nessuno dei due è ammissibile come motivo scientificamente valido per trarre una conclusione di qualsiasi tipo.
Ciò non significa che non si debba continuare a formulare tali teorie o a tentare di progettare esperimenti che possano rivelare o escludere la presenza di variabili nascoste; questo fa parte del modo in cui la scienza progredisce. Ma finora tutte queste formulazioni hanno portato solo a limitazioni e invalidazioni di specifiche classi di teorie a variabili nascoste. L’idea che esistano “variabili nascoste e che siano tutte codificate nel vuoto quantistico” non può essere esclusa.
Ma se dovessi scommettere su dove guardare dopo, noterei che nella teoria (newtoniana) della gravità sono presenti anche variabili coniugate: potenziale gravitazionale e densità di massa. Se l’analogia con l’elettromagnetismo (tra potenziale elettrico e carica elettrica libera) è valida, come ci aspettiamo, significa che possiamo ricavare una relazione di incertezza anche per la gravità.
La gravitazione è una forza intrinsecamente quantistica? Un giorno potremmo essere in grado di determinare sperimentalmente se questa incertezza quantistica esiste anche per la gravitazione. Se così fosse, avremmo la nostra risposta.
Ethan Siegel
Fonte: bigthink.com
SOSTIENICI TRAMITE BONIFICO:
IBAN: IT19B0306967684510332613282
INTESTATO A: Marco Stella (Toba60)
SWIFT: BCITITMM
CAUSALE: DONAZIONE










