IL Mistero della Bicicletta
Chi ogni giorno va in bicicletta non sa che ció che lo tiene in sella senza cadere è ancora un mistero tutto da scoprire.
Toba60
Meno dello 0,1% dei nostri lettori ci supporta, ma se ognuno di voi che legge questo ci supportasse, oggi potremmo espanderci e andare avanti per un altro anno.
Il mistero della bicicletta
Cosa c’è di così misterioso nell’andare in bicicletta? Ho imparato ad andarci, con un po’ di aiuto da parte di mio nonno Taddeo, quando avevo circa 5 anni. Sembrerebbe che non ci siano molte cose meno misteriose dell’andare in bicicletta. Ebbene, a quanto pare, la scienza del ciclismo rimane ancora in gran parte misteriosa, anche per gli stessi scienziati.
Questo mistero ha un nome: AUTOSTABILITÀ DELLA BICICLETTA.
Può essere difficile da credere, ma questo mistero potrebbe avere a che fare anche con l’antigravità quantistica.
Secondo la prestigiosa rivista scientifica Nature (23 dicembre 2015), il problema di andare in bicicletta ha quasi rotto la matematica! Jim Papadopoulos ha trascorso una vita a riflettere sulla matematica delle biciclette in movimento, iniziando da giovane ingegnere con il Bicycle Research Project della Cornell University all’inizio degli anni ’80.
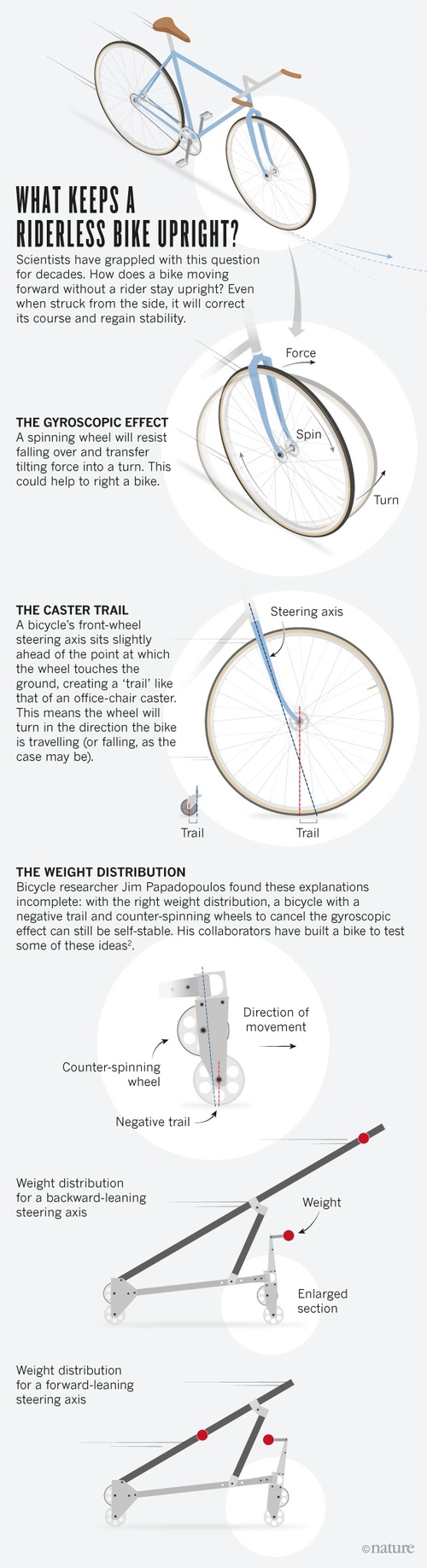
Come fa una bicicletta che avanza senza pilota a rimanere in piedi?
Gli scienziati sono alle prese con questa domanda da circa un secolo! Anche quando viene colpita lateralmente, corregge la rotta e riacquista la stabilità.

Se questo mistero della bicicletta può essere dovuto anche all’effetto giroscopico, allora dobbiamo chiederci: cosa spiega esattamente l’effetto giroscopico stesso. L’effetto giroscopico si spiega da solo? È ovvio? Se ci pensiamo bene, alcune delle cose più difficili da spiegare sono quelle ovvie, come ad esempio il tempo, lo spazio o lo spaziotempo.
Che cosa impedisce al giroscopio in rotazione di cadere sotto la forza di gravità mentre ruota (precessione) orizzontalmente?
Se rispondiamo a questa domanda, possiamo anche contribuire alla comprensione di:
Che cosa mantiene in piedi una bicicletta senza pilota?
Entrambe le domande sono simili nell’essenza. Le ruote della bicicletta non sono semplicemente due giroscopi? Pertanto, la mia risposta è che anche l’ANTIGRAVITÀ svolge il suo ruolo.
Nell’eccellente video qui sotto, una bicicletta molto stabile e autobilanciata viene presentata con l’affermazione che l’effetto giroscopico è stato eliminato grazie a due fattori, uno dei quali è la presunta cancellazione dei momenti angolari di entrambe le ruote. Se ciò fosse vero, ne conseguirebbe che le biciclette prive di momento angolare dovrebbero essere più stabili, come se l’effetto giroscopico dovesse essere un ostacolo alla stabilità.
Tuttavia, gli skibike non hanno ruote e rimangono comunque in piedi pur non avendo momento angolare! Possiamo quindi affermare con certezza che questo particolare “mistero” degli skibike si spiega da sé.
Da un certo punto di vista, possiamo dire che nel caso della bici del video i momenti angolari delle ruote si sono annullati. A mio parere, però, se i suoi momenti angolari fossero davvero fisicamente annullati (inesistenti), allora l’effetto antigravitazionale non potrebbe contribuire alla stabilità, come avviene nel caso di un giroscopio che gira orizzontalmente, mentre in questo caso la stabilità viene effettivamente aumentata.
Naturalmente, questo aumento di stabilità non può essere attribuito a un aumento del momento angolare. Può derivare solo dal fatto che le doppie ruote controrotanti della bicicletta hanno i loro momenti angolari orientati in direzioni opposte, il che contribuisce notevolmente alla sua stabilità.
Dal punto di vista matematico, la loro somma è zero (annullata), ma dal punto di vista fisico abbiamo ancora due forze opposte. Solo perché la loro somma matematica è zero, non ne consegue che siano fisicamente inesistenti. Questo è il motivo per cui l’effetto antigravità, agendo sul momento angolare di queste ruote a doppia rotazione, aumenta la stabilità della bicicletta.
Inoltre, è necessario distinguere due configurazioni di ruote a doppio controgiro. Quella che “annulla” più efficacemente i momenti angolari è quella in cui entrambe le ruote condividono lo stesso asse di rotazione. Nella configurazione della bicicletta del video, le ruote controrotanti non condividono lo stesso asse di rotazione.
Nel video, naturalmente, l’esperimento è corretto, ma questa particolare spiegazione non lo è. Guardate questo eccellente e sorprendente video:

Fonte: quantumantigravity.wordpress.com











